Quand on parle de chiffrement la question de le « casser » arrive généralement sur le tapis. Saviez-vous qu'il existe un (et un seul) système infaillible : le chiffre de Vernam. Il n'a rien de nouveau puisqu'il existe depuis des années et était notamment utilisé pour le fameux téléphone rouge entre Russie et Etats-Unis.
Comme tout le monde, vous vous êtes toujours demandé comment lancer un missile nucléaire en toute sécurité ou insulter le dirigeant d’en face sans que les Russes, les Chinois ou les Américains ne viennent perturber vos communications en changeant les cibles à l’insu de votre plein gré ou modifiant la teneur de l’insulte.
Plus sérieusement, vous vous êtes plus probablement demandé s’il existait un moyen de chiffrement infaillible et infalsifiable permettant la transmission d’un message de façon vraiment confidentielle ? La réponse est oui : le masque jetable est la meilleure des solutions, et c’est même la seule. Nous ne parlons pas ici de la covid mais du chiffre de Vernam.
Face à la révolution promise des machines quantiques...
Malgré de lourds inconvénients de mise en œuvre, cette solution a été utilisée de nombreuses années pour les échanges les plus confidentiels car, contrairement aux affirmations de mes amis du marketing (que j’adore évidemment), il s’agit bel et bien de la seule solution dont on peut garantir la sécurité.
En effet, on a prouvé mathématiquement que le chiffrement asymétrique à base d’entiers premiers serait cassé par des machines quantiques (si elles sont un jour capables d’implémenter l’algorithme de Schor et de factoriser rapidement des nombres entiers de grande taille).
Le chiffrement symétrique à base de clé secrète semble pour l’instant plus résistant aux petits atomes (quoique) mais il reste théoriquement attaquable par brute-force et même un peu plus facilement avec quelques méthodes d’amélioration dont les cryptanalystes ont le secret.
... le chiffre de Vernam reste inattaquable
Il est donc conceptuellement attaquable, même si pratiquement on ne disposera probablement jamais de la puissance de calcul nécessaire pour l’AES avec une clé de 256 bits, mais cela reste donc théoriquement possible.
Le chiffre de Vernam, lui, présente cette caractéristique unique d’être inattaquable. Nous en avions d'ailleurs parlé dans notre premier magazine (le #4 est en cours de financement sur Ulule). Même la force brute (tester toutes les combinaisons possibles) ne sert à rien, nous allons vous montrer pourquoi.
Les principes du masque
Un chiffre de Vernam (ou masque jetable, one-time pad en anglais) est constitué d’une très grande suite de lettres choisies totalement au hasard. Le hasard est un élément essentiel en cryptographie : il doit être le plus parfait possible car le moindre biais ou élément de prévisibilité peut affaiblir considérablement la force du chiffrement (voire l’annuler).
En pratique, il faut que cette suite de lettres soit au moins aussi longue que le message à chiffrer (rappel : on ne dit pas crypter). Chaque caractère est utilisé une fois et une seule : c’est pour cela que cette suite de lettres doit être au moins aussi longue que le message à chiffrer.
La plus complexe et la plus délicate des tâches sera de faire parvenir à son correspondant cette suite, qui doit donc être créée en deux exemplaires, un pour chaque correspondant, et là on rentre dans le domaine de la sécurité physique (ou sûreté).
Pour éviter de continuels échanges de masques jetables, qui doivent donc se faire physiquement et qui sont donc sources de risques, il est fréquent d’envoyer un masque assez long, qui sera utilisé jusqu’à épuisement.
Ainsi, s’il comporte 5 000 caractères, il pourra chiffrer 5 000 caractères de messages. Un premier message de 100 caractères utilisera les 100 premiers caractères du masque, un deuxième message de 80 caractères les 80 suivants, etc.
En pratique, pour chiffrer une lettre, on fait la somme avec la lettre correspondante dans le masque, modulo 26, et c’est tout ! Pour déchiffrer, on fait l’opération inverse : on soustrait.
Un exemple
On part d’un message de 4 caractères, "VRAI". Le caractère A correspond à 0, B à 1, etc. Pour le masque, on prend "YNPQ".
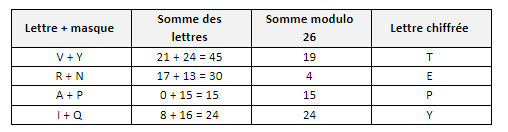
Le mot "VRAI" sera donc chiffré par "TEPY". Imaginons que je fasse maintenant de la force brute et que je teste (au hasard) le masque "OEVB".
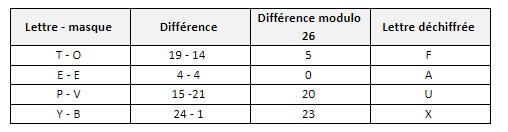
Si je prends le vrai message chiffré "TEPY" mais que j’utilise une mauvaise clé "OEVB", alors je déchiffre le message comme étant "FAUX" !
En conclusion, si vous testez toutes les combinaisons de 4 lettres pour le masque, vous lirez… toutes les combinaisons de 4 lettres possibles en sortie, avec parfois l’inverse du message initial, sans aucune possibilité de savoir s’il s’agit du message initial ou pas : seule la connaissance du masque utilisé vous donnera le bon message en sortie.
Pour vérifier tout ça, en Python très basique :

Remarquez au passage l’énorme complexité du programme de chiffrement / déchiffrement. Pas besoin d’un ordinateur quantique pour cela.
En pratique, sur des fichiers informatiques, on ferait plutôt du XOR sur le message codé en binaire (tout comme la clé), mais le principe restera le même.
Donc le masque est parfait, mais avec de fortes contraintes :
- la clé doit être plus grande que le message (pas très pratique) ;
- les lettres doivent être choisies avec un générateur d’aléas « parfait » ;
- on ne doit jamais réutiliser le masque (ou une partie du masque) ;
- la transmission du masque et son traçage (qui le détient, qui y a accès) sont des points sensibles mais relevant de la sécurité physique.
Pourquoi je ne peux pas réutiliser la clé ?
Vu la difficulté de transmission de la clé, on est vite tenté de réutiliser des parties de celle-ci. Or cette pratique est désastreuse : toute la sécurité du procédé vient du fait qu’il n’existe aucun lien entre le message et la clé.
Or réutiliser la clé revient à la relier aux messages, donnant ainsi des indications (au moins) sur une partie de la clé.
Téléphone rouge
On l’a compris, ce chiffrement est le seul qui permette des conversations réellement secrètes. Fort logiquement, on l’a utilisé pour le fameux téléphone rouge entre Washington et Moscou, en sachant que ce téléphone était en réalité un telex (terminal de transmission de texte) chiffré par ce procédé. Quant aux clés, elles voyageaient par voie physique, probablement par avion ou par valise diplomatique, loin de tous les regards.
La confidentialité est donc parfaite, mais avec des contraintes telles qu’en pratique le chiffre de Vernam est difficile à utiliser, particulièrement en informatique où la transmission de la clé ne peut pas passer par un canal numérique.









Commentaires (83)
#1
Super Intéressant !
J’en profite pour recommander au passage les vidéos de David Louapre (science étonnante) qui a fait quelques vidéos passionnantes sur les codes secrets …
#2
Dans le même genre (système inviolable), j’avais appris qu’avec un canal quantique en plus d’un canal numérique standard, il est théoriquement possible de se prémunir contre tout man in thé middle, le canal numérique étant sécurisé grâce à des données provenant du canal quantique et ce dernier étant… quantique, il est impossible de s’y brancher sans être détectable.
#2.1
Oui, contrairement aux ordinateurs quantiques qui ne sont pas encore au point (d’un point de vue industriel), on sait déjà transmettre (sur qqs centaines de km) une clé secrète par un mécanisme quantique. Et en effet quand on essaye de lire le signal, on le modifie, ce qui se voit avec un “simple” contrôle d’intégrité.
#2.2
Qu’est-ce qui fait que lire le signal quantique en modifie l’intégrité ? Merci
#2.3
Magie de la mécanique quantique : à chaque fois que tu “lis” l’état d’une particule, tu le modifies. Donc un contrôle d’intégrité montrera le problème à l’arrivée. Mais bon c’est dit de façon très simplifiée…
#3
Chouette article, néanmoins j’aimerais soumettre une petite modification de tournure de phrase ainsi que le changement du titre d’un autre article de
“Chiffrement : notre antisèche pour l’expliquer à vos parents”
à
“Chiffrement : notre antisèche pour l’expliquer à vos enfants”
ou éventuellement
“Chiffrement : notre antisèche pour l’expliquer à vos parents et enfants”
De petit geek curieux il y a ~25ans je suis passé à papa Geek depuis 6 ans ^^
#4
Quoi, pas de téléphone rouge Et le bouton rouge c’est aussi un mythe ?
Et le bouton rouge c’est aussi un mythe ? 
#5
Le code python, quasiment la même chose que le petit programme que l’on pouvait avoir dans quasiment tous les livres d’initiation au BASIC des années 80 et début 90 ! Bon par contre en général la clé était juste un nombre ou à la limite en utilisant le (très mauvais) générateur de nombres aléatoires.
#5.1
Le générateur de nombre aléatoires n’est pas mauvais, d’ailleurs il est similaire dans tous les langages (valeurs plus ou moins hardcodées), pour une raison simple : sauf scénario spécifique, on s’en fout d’avoir un nombre réellement aléatoire, il suffit qu’il paraisse aléatoire à l’utilisateur.
Générer un “vrai” nombre aléatoire est extrêmement coûteux en ressources, donc on ne le fait que lorsque c’est strictement nécessaire.
#6
La seule solution que l’on connaisse, ou bien c’est prouvé qu’il ne peut pas y avoir d’autres solutions infaillibles ?
#7
“le message à chiffrer (rappel : on ne dit pas crypter).”. Merci, peu savent faire la différence et utilise crypter pour chiffrer.
#8
Ça dépend quelques lampes à lave et une webcam suffisent
#8.1
Quand tu penses qu’une bonne partie de l’internet mondial est sécurisé par ce système
#8.2
Alors ça (lavarand) c’est un autre type de “coûteux en ressources”
#9
Si si, on peut dire crypter. La langue française est une langue vivante. Il est permis de modifier le sens de ses mots, voire d’ajouter de nouveaux mots. C’est l’usage qui décide quel mot reste ou pas. Si l’usage devient courant, il entre dans le dictionnaire.
N’en déplaise aux adorateurs de langue morte, dans ce cas - ci, c’est bien un combat d’arrière-garde.
#9.1
Le problème de crypter c’est que c’est un non sens absolu : tu chiffres avec une clé, tu déchiffres avec une clé, tu décryptes un message chiffré SANS avoir la clé de déchiffrement. Par conséquent, crypter devrait avoir le sens de “chiffrer” un message sans clé de chiffrement, ce qui revient juste à écrire un message random sans tenir compte du message d’origine, donc destruction total du message sans possibilité de décryptage.
Voilà pourquoi beaucoup ne sont pas favorables à son intronisation.
#9.2
Oui, la langue française évolue. Ce n’est pas pour autant qu’il faut négliger la signification des mots. Lorsqu’on s’adresse à un néophyte, utiliser crypter au lieu de chiffrer n’a que peu d’importance, les deux seront compris de la même manière.
Lorsqu’on parle technique, comme c’est le cas ici, et/ou à un lectorat averti (aussi le cas ici), la signification des mots prennent tout leur sens. Chiffrer existe, crypter n’existe pas dans le langage technique.
Déchiffrer et décrypter existent , et si ils représentent le même concept (traduire un message chiffré en un message lisible), les deux se font dans des contextes différents (déchiffrer = on possède la clé de déchiffrement, décrypter = on ne possède pas la clé de déchiffrement).
Utiliser crypter signifierait donc, comme le relève sephirostoy, de chiffrer le message sans connaitre la clé. Mais il existe un cas où la clé de chiffrement et la clé de déchiffrement ne sont pas les mêmes : le chiffrement asymétrique.
Pour ma part, avec le chiffrement asymétrique, on peut chiffrer un message sans connaitre la clé de déchiffrement (mais en connaissant la clé de chiffrement !). Donc, et pour le cas du chiffrement asymétrique, l’usage de “crypter” ne me paraitrait pas complètement déconnant, puisque cela reviendrait à chiffrer un message sans connaitre la clé de déchiffrement. Mais c’est un cas bien particulier et pour l’instant, pas vraiment d’usage auprès des avertis.
#10
En théorie un message “crypté” est un message dont personne ne comprend le contenu, par exemple les écritures d’une civilisation ancienne, contrairement à un message chiffré qui est obtenu par calcul avec une clé/table/….
Donc oui la langue évolue et je suis 100% pour, mais là on a des mots qui signifient deux choses fondamentalement différentes, “l’évolution” de la langue reviendrait ici donc non pas à donner un nouveau sens à un mot, créer un nouveau mot ou entériner une expression courante qui ne relevait pas du “bon usage” de la langue, mais à confondre deux termes et appauvrir le vocabulaire.
Du coup à mon humble avis sur ce cas précis ce n’est pas un “combat d’arrière garde” mais un combat pour garder la richesse et la précisions de la langue Française et permettre la distinction entre deux situations à l’aide de deux mots différents.
#10.1
Mais du coup quid des cryptomonnaies, attestées par l’usage ?
J’veux bien causer de “chiffromonnaies” mais ça fait un peu crypto-réac.
#10.3
Ben ces des monnaies auxquelles personne ne comprend rien
#10.2
On emploiera plutôt « cryptique » que « crypté » pour désigner une vieille écriture incompréhensible.
Il n’en reste pas moins que chiffrer est très largement préférable (et le terme utilisé par tous les gens du domaine), du fait de la distinction déchiffrer / décrypter qui a déjà été évoquée.
#11
De même, ça me hérisse le poil d’entendre “digital” au lieu de “numérique” ou “clôturer” pour “clore” ou “fermer”.
#12
Concernant la clé jetable. Les USA ont depuis des années pris le parti d’enregistrer le bruit diffus cosmologique afin de pouvoir “cassé” d’éventuelle message l’utilisant comme “clé”…
Et c’est la, je pense la “presque” faille du système. La création de la clé.
Sur un message unique et court, oui c’est mission impossible pour des échanges réguliers créer ou trouver une clé est toujours une gageure.
#13
Le “crypto” de “cryptomonnaie” vient de “cryptographie” (qui est la base des cryptomonnaies), pas “crypter”.
#14
Générer un vrai nombre aléatoire avec un système déterministe est effectivement très problématique et couteux. En chiffrement, un générateur de nombre pseudo-aléatoire est un risque, dans le pire des cas, avec un mauvais algo, un adversaire peut prédire le chiffre qui sera généré ou réduire la surface à couvrir avec l’attaque force brute… et des mauvais algos il y en a eu au cour des 40 dernières années, y compris le fameux Dual_EC_DRBG validé en 2006 par la NSA et poussés par le NIST *.
Heureusement, de nos jours, le matériel incorpore de plus en plus souvent un générateur de bruit servant de source d’entropie pour générer des nombres aléatoires en continu.
*Bon, le coup du Dual_EC_DRBG est particulier car si on lit les brevets déposés par Certicom, on voit que la “faiblesse” était une fonctionnalité introduite pour faciliter la récupération de données sur une flotte de systèmes mobiles chiffrés individuellement… la NSA ne pouvait pas ignorer ce fait, et c’est pour cela qu’il ne faut plus faire confiance aux standards du NIST et toujours se référer à des cryptanalystes et mathématiciens réputés avant d’adopter un standard pour son entreprise.
#15
Sympa cet article.
Ceci dit, une clé qui soit plus longue que l’ensemble des données à chiffrer (un fichier texte de 2Ko avec une centaine de couples login/mot de passe) est une gageure. Elle ne peut raisonnablement être retenue et saisie au clavier par l’utilisateur. C’est donc une clé qui est stockée dans un fichier quelque part dans l’ordinateur. La faiblesse est là je pense.
Perso, je suis à la recherche d’un executable windows qui s’ouvre avec un mot de passe fort, et qui permette d’editer son contenu comme un notepad, puis se referme et s’autorechiffre avec la clé. Rien trouvé de satisfaisant dans l’open source jusqu’à présent.
#16
Tu peux peut être regarder du coté d’ansible. Il y a la notion d’un coffre fort avec édition de fichiers chiffrés. L’éditeur utilisable est configurable. Par contre, je ne sais pas si l’ouverture peut se faire autrement qu’en ligne de commande…
https://docs.ansible.com/ansible/latest/user_guide/vault.html#editing-encrypted-files
#16.1
Merci pour l’info, mais pas envie de chiffrer un dossier conteneur,
ni envie de tâter de la ligne de commande, étant donné que je dois accéder au fichier mot de passe 5 à 10 fois par jour (je refuse que Vivaldi ou Iridium stockent mes mots de passe).
En fait, j’avais trouvé cela, mais le logiciel semble abandonné (pas de M.A.J depuis 12 ans).
https://fsekrit.fr.uptodown.com/windows
https://progsoft.net/fr/software/fsekrit
#16.2
Si c’est pour gérer des secrets, pourquoi ne pas utiliser un gestionnaire dédié comme KeepassXC ?
#17
A un moment, j’utilisais GnuPG Vim … ça marche assez bien dans l’ensemble…
#18
Ceci suppose que le masque et le message sont transmis par deux voies différentes ; sinon il suffirait d’appliquer l’un sur l’autre. Mais si l’espion accède aux deux voies il peut déchiffrer le message. Le mode de transmission du masque me semble plus important que la méthode de chiffrement. Un peu comme si on plaçait sa clé à côté d’une serrure ultra-sécurisée.
#19
Un autre exemple de l’utilisation du chiffrement de Vernam:
Fidel Castro et Ernesto « Che » Guevara se sont retrouvé un soir dans un bar.
Ils avaient chacun un carnet et ont tiré au dé les caractères du masque en faisant croire qu’ils jouaient à un jeu du style 421 en notant tout les deux le résultat.
On a réussi à déchiffrer leur message à la mort de Guevara quand on a récupéré son carnet.
Je dit déchiffrer car on avait la clé.
Comme dit dans l’article, en français chiffrer et déchiffrer se font avec la clé, décrypter se fait sans, crypter n’existe pas car on ne peut chiffrer sans clé.
#20
Ben si, le message est crypté pour toute personne ne possédant pas la clé.
#20.1
Déjà tu compares un verbe (crypter) et un adjectif (crypté)…
Et on dit qu’il est chiffré (que l’on possède la clé ou pas ne change rien à ce fait).
#20.2
Tu cryptes ton message pour toutes les personnes indésirables et tu le chiffres pour ton interlocuteur, je ne vois pas où est le problème.
#20.3
Deux mots pour décrire la même action, c’est fort…
#20.4
Quand je pisse ou quand j’urine je fais la même chose…
#20.5
Pisser est populaire et vulgaire, contrairement à uriner, tu ne dis donc pas la même chose
#20.6
Et puis on peut “pisser du code”, mais je n’ai jamais entendu “uriner du code”

#21
Il me semble que pour les communications avec certains satellites militaires, on utilise (ou on a utilisé) un chiffrement de Vernam, avec une clé “infinie” pseudo-aléatoire générée algorithmiquement (et les générateurs doivent donc être synchronisés de chaque côté).
#22
Ce mode de chiffrement est un oublié de l’IoT, un petit article il y a 7 ans sur mon blog : http://guerby.org/blog/index.php/2015/05/26/217-internet-of-things-and-one-time-pad
#23
la cryptographie en cryptomonnaie ne sert pas à chiffrer un message mais à valider une authenticité/unicité. ce qu’on appelle la preuve
#24
Alors c’est pas le cas d’usage initial mais password-store permet de rentrer du champ libre sans limitation en plus du mot de passe. C’est chiffré automatiquement avec ta clé PGP. Et bien entendu il faut ta clé PGP pour déchiffrer le texte. (donc le mot de passe fort est celui de ta clé PGP)
Sous windows le client c’est qtPass ou pass4Win
#25
C’est quand meme difficile de trouver plus complet et qualitatif que les recommendations du NIST. Un cryptologue réputé ne te dira jamais de préférer sa solution aux standards, sauf cas tres particuliers. Une entreprise qui aurait une telle stratégie est assurée de ne jamais gagner un gros contrat.
#26
J’ai jamais compris le troll “on dit pas crypter mais chiffrer”: les deux sont admis par les dictionnaires Larousse et le Robert. J’imagine que les adeptes de chiffrer n’utilisent jamais d’anglicisme dans leurs courriels, sur leur micro-ordinateur connecté au commutateur de leur FAI.
#26.1
D’autant que ça ne vient pas de l’anglais mais du grec https://fr.wiktionary.org/wiki/%CE%BA%CF%81%CF%85%CF%80%CF%84%CF%8C%CF%82
#26.2
Je pense que le “troll” vient de l’association chiffrer à déchiffrer et de crypter à décrypter.
Déchiffrer et décrypter veulent dire deux choses similaires mais différentes : retrouver le message initial en connaissance (déchiffrer) ou non (décrypter) la clé de déchiffrement.
Certains “puristes” se refusent donc d’utiliser crypter pour dire chiffrer car chiffrer sans connaitre la clé n’a pas de sens pour eux.
Sauf que, comme je le relevais plus haut, si on considère que comme décrypter, c’est “déchiffrer” sans connaitre la clé de déchiffrement, crypter pourrait être considéré comme “chiffrer” sans connaitre la clé de déchiffrement.
Cela n’a pas de sens pour du chiffrement symétrique (car clé chiffrement = clé déchiffrement), mais peut avoir du sens dans le cadre d’un chiffrement asymétrique.
#26.3
Bonjour,
les deux existent.
Cependant pour moi la différence est la suivante : Crypter tu ne possède pas le code ; Chiffrer tu le possèdes.
La conséquence ?
C’est que si tu cherche l’action inverse, tu ne pourras pas pour le 1er, et du devrais essayer de faire du décryptage (comme un pirate donc) et rien ne dit que tu pourras y arriver (en tant humain raisonnable) alors que pour le second tu ferras du déchiffrement et donc sera bcp plus “simple” et rapide pour toi.
J’espère avoir un peu, expliciter le pourquoi d’être tatillon de certains sur le sujet.
Après chacun fait comme il le sent.
#27
Chiffrer / déchiffrer, crypter / décrypter, les deux sont acceptables. Pour “crypter”, le terme vient du grec “kruptein” qui signifie “cacher”, ainsi la crypte d’une église n’était accessible qu’à certains et restait cachée pour la majorité des fidèles. Certes “crypter” ne contient pas l’idée de chiffres qui permettent de cacher le sens, mais “chiffrer”… ne contient pas l’idée de cacher. Donc aucun des deux termes ne convient parfaitement. Match nul. La seule réserve que je ferais concerne l’emploi : dans un même texte - ou article - il faut choisir et employer soit chiffrer / déchiffrer soit crypter / décrypter.
#28
Tu n’as pas du vivre la guerre des générateurs pseudo aléatoires fin 90/début 2000: avec comparaison de la distribution des nombres générés, analyse des nombres dont on a une bonne chance de connaître le suivant, boucles, …
‘Deviner’ un nombre pseudo aléatoire à partir du nombre précédent et de l’os (rip SUN OS) pour faire de l’IP spoofing…
Même les via c3 ont eu leur générateur intégré basé sur une interférence dans le CPU…
Ne pas oublier les enseignements des sages: ne pas sous estimer les d’ailes du générateur pseudoaléatoire
#29
C’est clair. Ce n’est pas un algo adapté à toutes les situations: devoir transférer de façon sécurisée une clé de la taille des données, ce n’est pas toujours simple. La majorité de nos usage de chiffrement, c’est justement pour sécuriser un lien qui ne l’est pas d’origine.
Et devoir stocker/transférer deux fois les données (en taille), ce n’est pas souvent souhaitable…
Par contre, ça a été utilisé pour des dongles, plus ou moins pour la sécurisation de la n64, …
#30
Non, toujours pas.
On chiffre un message, point barre. Ensuite c’est pour le décoder qu’on peut déchiffrer ou décrypter.
Dans l’asymétrique, la clé de chiffrement est connue, donc non ca n’a pas de sens non plus.
#31
Mais du code à chier certainement
#32
Il fera son boulot et commentera sur base des recherches académiques sur
le sujet. En l’occurrence, les algos de la suite B du nist étaient déjà critiquées avant de devenir des standards officiels. Quand la nsa a en plus rendu l’emploi du générateur aléatoire DUAL_EC_DRBG pour ceux qui voulaient utiliser les brevets sur le reste du nouveau standard NIST, nombreux sont ceux qui se sont inquiétés d’une manœuvre de la NSA pour affaiblir globalement les standards de chiffrement.
Du coup , le reste de la suite B a été examiné à la loupe, et une partie du santdard a été mis à la poubelle. De son côté, la communauté s’est recentrée sur des alternatives disposant de meilleurs preuves mathématiques comme, par exemple, les courbes 25519 et ed 25519.
#33
Les développeurs seront contents qu’on les appelle “programmateurs” parce que le public ne fait pas la différence entre programmeur et programmateur…
Les termes scientifiques (l’informatique et la cryptographie sont aussi des sciences) ont sens défini pour qu’ils soit compris formellement. En crypto, on chiffre, on déchiffre, on décrypte, mais on ne crypte pas, et on n’encrypte pas, même si les journalistes et le public utilisent ces termes.
#34
Crytopgraphie (nom féminin) : étude des usages de deux mots dans la langue.
#35
Donc, en gros, c’est un chiffre de Vigenère avec une clé plus grande que le message.
#36
T’as essayé CheeryTree ? https://www.giuspen.net/cherrytree/#features
Ou le mécanisme ne t’as pas plu ? “password protection (using http://www.7-zip.org/) – NOTE: while a cherrytree password protected document is opened, an unprotected copy is extracted to a temporary folder of the filesystem; this copy is removed when you close cherrytree”
Moi, à défaut de mieux, j’utilise cela
#37
Non, c’est juste garder le sens des mots.
Certains dictionnaires entérinent des formules qui sont incorrectes (ou des anglicismes nets, comme “encodage” - berk), le Robert est particulièrement laxiste je trouve.
Même remarque que plus haut.
Malheureusement les dictionnaires se font “avoir” par le fait que l’anglicisme pourrit l’informatique.
Haha oui parfois.
Il faut dire que même dans le milieu informatique, il y a une proportion notable qui n’a pas un super niveau en français (ou en anglais) et qui ne se rend pas compte des anglicismes et autres abus de langage.
J’ai à coeur de parler bien le français ET bien l’anglais, autant que possible, sans mélanger.
#37.1
Juste une remarque, crypter c’est du grec ancien, pas de l’anglais.
Et coder/décoder ça existe aussi en français.
#38
Keepass ?
#39
Oui mais les anglais utilisent “to crypt” comme déjà dit plein de fois précédemment.
Je n’ai jamais dit le contraire.
C’est “encoder” / “encodage” qui est beurk en français (car on dit “coder” et “codage” en bon français et en math).
#39.1
On sent fou de ce que disent les anglais.
Les anglais disent “déjà-vu” tu vas l’interdire en français ?
Crypter existe en français (sauf pour patch) parce que c’est un mot d’origine grecque.
Tu cryptes pour rendre inintelligible, tu chiffres pour rendre confidentiel, je ne vois pas où est le problème.
Quand j’enregistre des fichiers dans un conteneur stormshield, les données ne sont chiffrées que pour moi (ce qui dans l’absolu est absurde), c’est bien pour crypter les données.
#40
N’importe quoi
On ne “crypte” pas, on a déjà expliqué pourquoi.
On chiffre des données.
On va arrêter le troll là.
#41
En tandhruilien, ca existe peut-être. En francais, non, certainement pas.
On est plein à t’avoir expliqué pquoi ici, OlivierJ a eu la (grande) patience de te l’expliquer encore une fois…
#42
Coder et décoder n’ont pas du tout le même sens que chiffrer et déchiffrer, ni le même contexte. Les algos de codage et décodage interviennent en traitement du signal (manchester, arinc…), alors que chiffrement et déchiffrement c’est en cryptographie. Et quand on mélange les deux, c’est de la transmission chiffrée (par exemple téléphone sécurisé) : chiffrement => codage => transmission => décodage => déchiffrement.
A vouloir changer le sens des mots on finit par s’emméler les pinceaux (et passer pour une buse auprès des professionnels).
#42.1
Tout à fait, c’est sans doute pour ça que les décodeurs canal plus étaient autant piratés.
Sinon, quand tu dis que tu es professionnel c’est parce que tu travail au Littré, pour l’académie ou tout au moins comme correcteur ?
#43
Vous n’avez rien compris, on dit masquage/démasquage en français.
On démasque un usurpateur qui essaye de se cacher.
Pas pour rien que l’opération la plus utilisée par les algo de chiffrement soit le XOR, soit l’application d’un masque.
#44
D’ailleurs, en anglais, il y a bien les mêmes termes qu’en français, à savoir :
to cipher : chiffrer
to uncipher : déchiffer
to uncrypt : décrypter
#45
Bon article explicatif. Le chiffre de Vernam est en effet quelque chose qui est théoriquement inviolable (même si on a une puissance infinie pour faire une attaque par force brute, comme l’évoque l’article), et qui pourtant reste très simple (il est basé sur un simple XOR)
Cependant, je trouve dommage que l’article n’évoque pas plus que ça les défauts du chiffre de Vernam, qui le rendent difficilement utilisable en pratique.
Le problème avec le chiffre de Vernam est que ça reste du chiffrement symétrique (on utilise la même clé pour chiffrer et déchiffrer, contrairement à du chiffrement asymétrique où les clés pour chiffrer et déchiffrer sont différentes), et le chiffrement symétrique seul est par nature très difficile à utiliser dans un contexte d’échange d’informations entre deux correspondants : il faut qu’on puisse s’échanger les clés, qu’elles soient entièrement aléatoires, qu’on soit sûrs de bien utiliser le bon morceau de clé quand on veut chiffrer/déchiffrer quelque chose…
Cet article évoque très bien les différentes contraintes du chiffre de Vernam (et plus largement du chiffrement symétrique) : https://blog.imirhil.fr/2016/03/12/chiffrement-vernam.html
Le chiffre de Vernam reste toutefois utile dans un contexte où la donnée ne va pas être envoyée quelque part (archive, stockage…), mais le rapport sécurité / contraintes fait qu’il n’est pas forcément plus intéressant comparé à un algorithme classique tel que AES-256.
#46
Non j’ai un master degree en monétique et sécurité des systèmes (dont cryptographie), j’ai travaillé avec le groupement des cartes bancaires et dans la sécurisation des smartcards (mise en place des algos de chiffrement), dans le traitement du signal avionique et militaire (codage/décodage).
Le décodeur canal+, il déchiffre le flux avec la carte à puce de l’abonné, flux issu d’un signal décodé par le récepteur, mais niveau marketing le “déchiffreur canal+” ça passait moins.
#46.1
Ce que j’essaye de t’expliquer, c’est que ce n’est pas parce que tu connais 1 définition de coder/décoder que ça en fait LA définition.
https://www-fourier.ujf-grenoble.fr/~parisse/giac/doc/fr/casrouge/casrouge012.html
#47
Le codage CESAR n’est pas un chiffrement, il n’y a pas de clé. Juste un algorithme qui est le même pour tout le monde.
#47.1
La clé c’est pas la valeur du décalage justement.
#48
Une fois connu, un codage n’offre aucune sécurité, contrairement à un chiffrement.
Le ROT13 est un codage aussi. Par contre ENIGMA n’en est pas un, il y une clé.
#48.1
Il n’empêche que le message reste crypté pour celui qui ne connait pas le code.
#49
Et donc, tout texte écrit dans une langue que tu ne connais pas est cryptée ?
A partir de ce moment-là, je peux me défendre en justice pour une app pourrie où j’enverrais des données sensibles en clair sous prétexte que le format ne suis aucun protocol connu par d’autres et que donc je les envoie pas en clair en fait, mais de manière cryptée ? .
.
Un texte “altéré” (par chiffrement, par corruption, …) n’est pas crypté à partir du moment où tu as la nécessité de le décrypter pour en retrouver sa forme non alterée mais à partir du moment où il aurait été “crypté” (en admettant que cette action existe). Un document chiffré avec une clé, ne devient pas crypté lorsqu’il est entre les mains d’une personne qui ne possède pas la clé de déchiffrement, ça reste un document chiffré, mais il aura à faire du décryptage pour en récupérer le texte originel.
L’adjectif “crypté” s’applique au fait qu’il ait subi une action de cryptage (adjectif participe passé). Et si on considère que “cryptage” soit l’opposé de “décryptage”, cela revient à créer sciemment un texte que personne ne pourra déchiffrer pas même l’auteur (par ex, tu écris un roman qu’avec la touche ‘a’ de ton clavier, c’est assez efficace pour faire du texte crypté, mais un non sens absolu).
#50
A première vue c’est efficace
https://www.curieuseshistoires.net/les-americains-utilisaient-le-navajo-durant-la-seconde-guerre-mondiale/
#50.1
C’est marrant parce que ton exemple ne concerne pas des textes dans une langue étrangère, mais l’usage de mots d’une langue étrangère comme un code. Le document produit n’est donc pas valide dans la langue utilisée. As-tu seulement lu l’article que tu partages ? ^^’
Et de ce fait, ça en fait des documents codés, et non chiffrés. Et encore moins crypté, on te l’a déjà expliqué, cela n’a pas de sens., surtout pour s’envoyer des codes militaires…
#51
Je cite le premier paragraphe
Donc pour les forces de l’axes qui ne connaissent pas le Navajo (une langue étrangère), le message est crypté (participe passé du verbe crypter).
#51.1
Oui si “CurieusesHistoires” dit que c’est un système de cryptage alors c’en est un
#52
Disons que pour envoyer un mot, tu convertisses chaque lettre par un mot de la langue française correspondant. Cela n’en fait pas un texte en français, c’est ce que je tente de t’expliquer. Donc, non, ton exemple ne concerne pas un texte en langue étrangère, mais un document codé au moyen de mots d’une langue étrangère. Mais bon, les subtilités ne semblent clairement pas ton point fort.
https://xkcd.com/257/
#53
Mon point c’est qu’en dehors de la France et qq pays francophones, ce débat n’a strictement aucune utilité.